About PaCSTCL's Grammar
Written by: Kimberlee Model, posted: 2019-10-09. Tags: I Made a Thing, Programming Language Development, Computing Thoughts, Computer Science Education.In September I spent a lot of time with the grammar of PACSTCL. Both in developing the grammar further than I had coming out of the CSforALL Bootcamp, and in preparing the PACSTCL code to parse the grammar. This post is going to start out by defining computer grammar in understandable terms, then it will go into some of the decisions going into and the quirks coming out of PACSTCL's grammar.
Like human language, computer languages require rules which define what statements are understandable and what statements are gibberish. Human languages are somewhat lax and easy to parse -- by humans, although there are some devotees who impose rigid standards of grammar on others. This is possible because humans use creativity to fill in gaps where a sound bite is lacking. Computers cannot do the same, and thus must rely on very rigid rules to interpret language.
The basis of computer language processing is the conversion of a sequence of tokens into a more complex structure. Tokens (sometimes used semi-interchangeably with "symbols") can be of various natures: they can be single ASCII characters or Unicode code points, or they can be keywords and identifiers. Regardless of their structure, these are the building blocks of computer grammars.
Grammars themselves are classified by the structures they produce. Lets take a look.
Regular Expressions
The grammar class that many people are already somewhat familiar (Don't worry if you aren't I'll explain) with are regular expressions (or regex for short). These are the simplest types of grammar: they consume sequences of tokens and produce the same sequence of tokens. Sounds kind of dumb, but while they're doing just about nothing they will also indicate whether a particular statement is allowed or not allowed.A regex uses just a few tools to recognize valid sequences. Most commonly sequences of characters, but they can be used for other sequences too.
- Character Classes
-
Match exactly one occurence of a character.
The regex
awill match the single lettera. But a class can match a choice of different letters, typically notated by square brackets with ranges or sequences.[aA]will match eitheraorA,[a-z]would match any single lowercase letter, and[a-zA-Z]would match any letter, but not numbers or symbols..is often used as a special character class which matches any character. - Repetition
-
In a regular expression, the "klene star" (or asterisk) indicates that whatever precedes it can be repeated zero or more times.
So if I have
a*, then I match,aandaaaaaaa. - Alternatives
- An alternative regex indicates that it matches either one sub-regex, or another. The two sub-regexes are separated by a pipe (
|), like thisa|b. This would match eitherab - Embedded Regexes
- An embedded regex is simply a parenthesized regex to break order of ops. For example
a*|a(b*|c*)in this case, removing the parenthesis would change the meaning of the regex, instead of matchingaccit would matchccc. It also can be used for repeated sequencesabc(def)*. - Sequences
- Allow one regular expression to be followed by another regex.
exactwould match an the wordexact, and[A-Z][a-z][A-Z][a-z][A-Z][a-z]would match a sequence of six letters TyPeD oBnOxIoUsLy.
These all come together to create pattern matchers. For example, this will match most valid email addresses:
[a-zA-Z0-9]([a-zA-Z0-9.+_-]*[a-zA-Z0-9]|)@([a-zA-Z0-9][a-zA-Z]*\.)*[a-zA-Z0-9][a-zA-Z]*\.[a-zA-Z0-9][a-zA-Z0-9]*
In the username portion, it starts out as a single alphanumeric character, followed by either many alphanumerics and symbols with a final alphanumeric, or an empty string. The domain name (after the @ sign) is a little more complicated. I'll leave it as an excercise to figure that one out.
Regular Expressions in PaCSTCL
PaCSTCL uses regexes in a compiler subsystem, or phase, called the "lexer". This phrase's job is to break source files, which are long sequences of letters, into individual words and symbols, or tokens. In theory, PaCSTCL will begin match the beginning of the source file against a regular expression, and the matched input is the basis of the first token. In practice, it is a little more complicated. For a few reasons, you'll never find any actual regular expressions in the source code (perhaps in the comments), Instead, you'll find a directed graph of states, through which it traverses as it scans each character. This is called a Deterministic Finite Automata, and it is the same data structure which is commonly used to implement regex parsers.
However, it has some extensions. Depending on the path it took to match a given input, it will output two things: the input itself, and an enumeration of what kind of input it is: an identifier, numeric literal, the if keywords, etc.
Moreover, given that it matches one in a multitude of regular expressions, if one were to write out the regular expression for PaCSTCL's lexer, it would read somewhat like this.
and|boolean| . . . |==|+|*| . . . |[0-9][0-9]*|[a-zA-Z][a-zA-Z]*
Context Free and Context Specific Grammars
Clearly, regexes alone aren't enough to define a language. A context free grammar (CFG) is the class above regular expressions, and it transforms a sequence of tokens into a tree of tokens: known as the Abstract Symbol Tree (AST). The basic unit of a CFG is the production. On the left hand of a production is its name, and on the right is a set of terminals and nonterminals.
A terminal is a single symbol, one of the sub-regexes from the lexer.
For clarity, I separate these into simple tokens: matching an exact string, and complex tokens: matching any other regular expression.
I notate simple tokens by simply quoting them, and complex tokens by naming their definition on another line, and referrring to their name, surrounded by square brackets ([name]).
Terminals, as implied by their name generate "terminating" nodes in the AST.
These are the tree's leaves - or nodes with no children.
Nonterminals, since they don't "terminate" have children nodes -- they create new layers in the tree.
Each nonterminal is defined by one or more productions.
And anywhere that a nonterminal is used as a production, then the AST of one of its productions can be used as a child node.
I notate nonterminals by their name, surrounded by angle brackets (<name>).
Lets take a look at a simple expression parser.
<expr> -> <expr> "+" <expr>
<expr> -> <expr> "-" <expr>
<expr> -> <expr> "*" <expr>
<expr> -> <expr> "/" <expr>
<expr> -> [identifier]
<expr> -> [numeric]
[identifier] -> [a-zA-Z_][a-zA-Z0-9_]*
[numeric] -> [0-9][0-9]*(|\.[0-9][0-9]*)
Given this simple grammar, and their a priori knowledge of basic arithmetic, one would expect this to generate the following AST for the expression m * x + b:
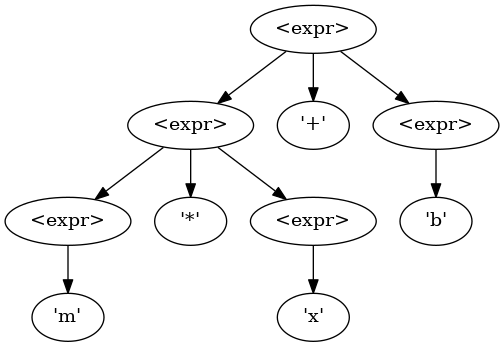
m * x + b using PEMDAS order of operations.
Using a recursive tree-walk to interpret this,
the interpreter would first interpret m * x.
Then it would interpret <result> + b.
However, this is also a valid parse tree, and could be generated by a parser:
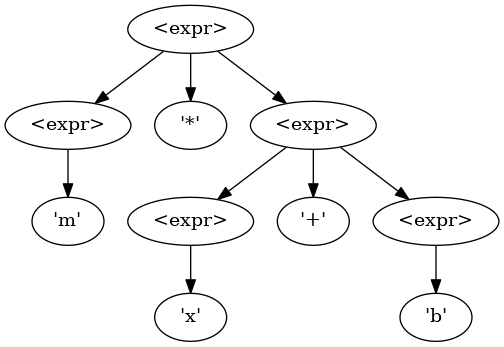
m * x + b is gramatically valid, however mathematically would produce the wrong results.
In order to fix this, we'll have to split the <expr> nonterminal up, and muck around with the grammar.
In PaCSTCL's grammar, I've been using this as an idiom for binary infix expressions (normal math notation).
<add-expr> -> <add-expr> "+" <mult-expr>
<add-expr> -> <add-expr> "-" <mult-expr>
<add-expr> -> <mult-expr>
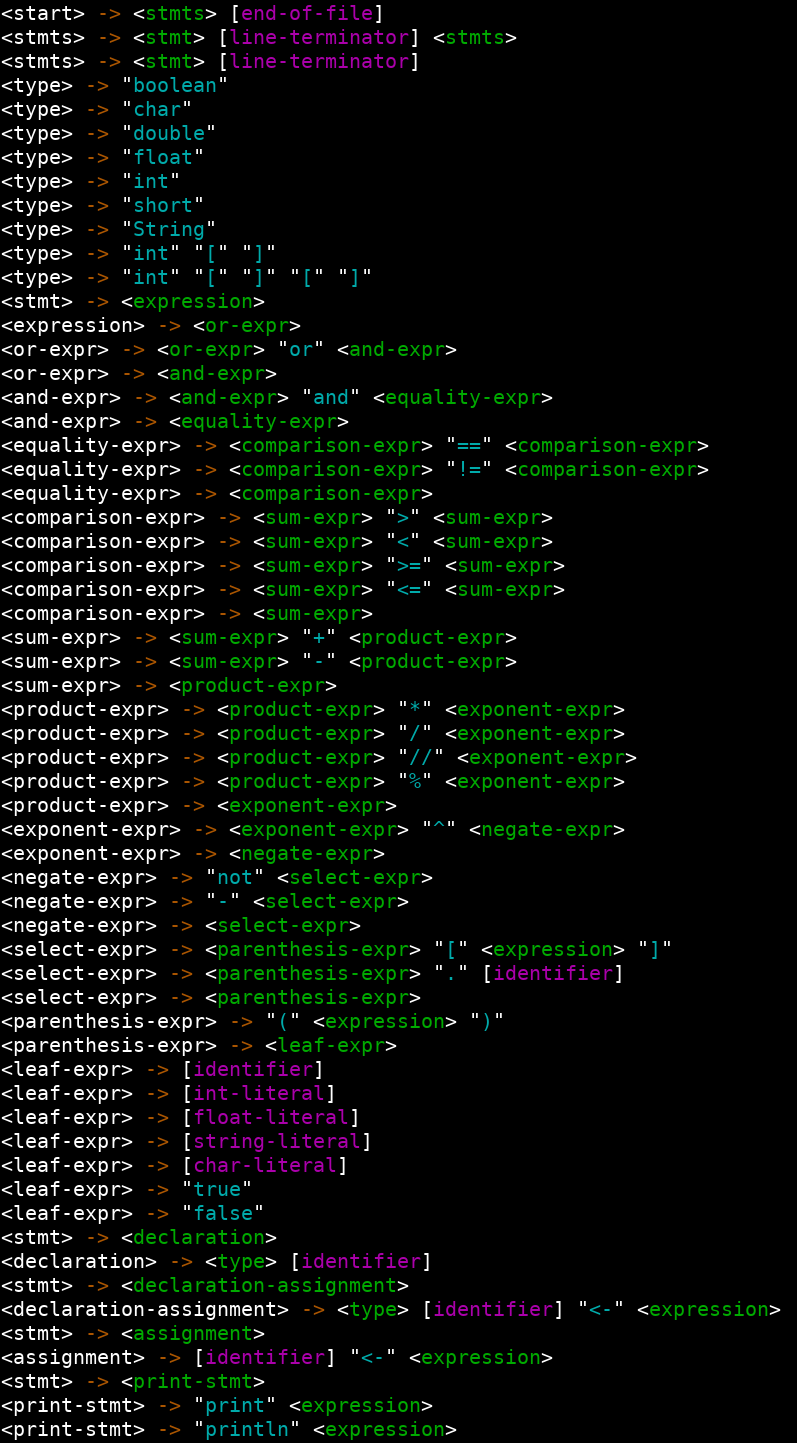
This pattern does two things: it encodes order of operations into the grammar -- by making the unwanted version of the parse tree invalid, and it enforces left-to-right evaluation. Here is a more comprehensive example, coming from my senior project, N-Lang. And of course, here is a print out, with color-coding of PaCSTCL's grammar as of October 2019.